Lời giải của Tự Học 365

Hàm số \(y = a{x^4} + b{x^2} + c\) có \(a < 0,b = 0,c > 0\) nên có \(1\) cực trị và chính là điểm cực đại.

Đồ thị có dạng như sau:

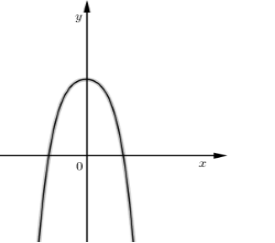
Quan sát đồ thị ta thấy:

- Đồ thị hàm số cắt trục hoành tại \(2\) điểm phân biệt nên A đúng, B sai.

- Đồ thị hàm số chỉ có \(1\) điểm cực đại và nó nằm ở phía trên của trục hoành nên C đúng.

- Đồ thị hàm số đi qua điểm \(\left( {0;c} \right)\) và \(c > 0\) nên nó không đi qua gốc tọa độ.

Đáp án cần chọn là: b