Lời giải của Tự Học 365

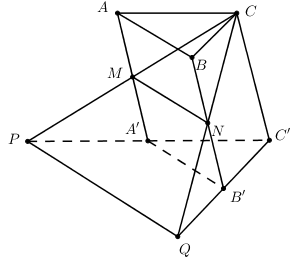
Gọi diện tích đáy, chiều cao, thể tích của hình lăng trụ ABC.A’B’C’ lần lượt là \(S;\;h;\;V \Rightarrow V = Sh\).

Ta có: \(\Delta A'B'C' \sim \Delta PQC'\) theo tỉ số \(\frac{1}{2} \Rightarrow {S_{C'PQ}} = 4{S_{A'B'C'}} = 4S.\)

\( \Rightarrow {V_{C.C'PQ}} = \frac{1}{3}.h.4S = \frac{4}{3}V\).

Ta có : \({S_{ABNM}} = \frac{1}{2}{S_{ABB'A'}} \Rightarrow {V_{C.ABNM}} = \frac{1}{2}{V_{C.ABB'A'}}\)

Mà \({V_{C.ABB'A'}} = \frac{2}{3}V \Rightarrow {V_{C.ABNM}} = \frac{1}{2}.\frac{2}{3}V = \frac{V}{3} \Rightarrow {V_{CC'A'B'NM}} = V - \frac{V}{3} = \frac{2}{3}V\)

Vậy \({V_{A'MPB'NQ}} = \frac{4}{3}V - \frac{2}{3}V = \frac{2}{3}V\).

Đáp án cần chọn là: d