Lời giải của Tự Học 365

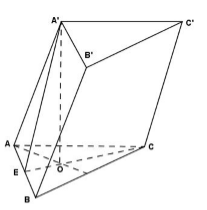
Gọi E là trung điểm của AB ta có:

\(\left\{ \begin{array}{l}OE \bot AB\\A'O \bot AB\left( {A'O \bot \left( {ABC} \right)} \right)\end{array} \right. \Rightarrow AB \bot \left( {A'OE} \right) \Rightarrow AB \bot A'E\)

Tam giác vuông A’EA có \(\widehat {A'AE} = {45^0} \Rightarrow \Delta EAA'\)vuông cân tại E\( \Rightarrow EA' = EA = \dfrac{a}{2};AA' = \dfrac{{a\sqrt 2 }}{2}\)

Tam giác ABC đều cạnh a nên \(CE = \dfrac{{a\sqrt 3 }}{2} \Rightarrow OE = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{6}\)

\(A'O \bot \left( {ABC} \right) \Rightarrow A'O \bot OE \Rightarrow \Delta A'OE\) vuông tại O

\( \Rightarrow A'O = \sqrt {A'{E^2} - O{E^2}}  = \sqrt {\dfrac{{{a^2}}}{4} - \dfrac{{{a^2}}}{{12}}}  = \dfrac{{a\sqrt 6 }}{6}\)

Tam giác ABC đều cạnh a nên \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)

Vậy \({V_{ABC.A'B'C'}} = A'O.{S_{ABC}} = \dfrac{{a\sqrt 6 }}{6}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 2 }}{8}\)

Đáp án cần chọn là: b