Lời giải của Tự Học 365

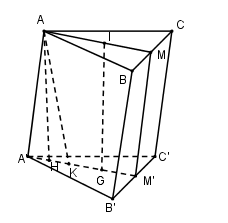
Gọi M’ là trung điểm của B’C’, \(K \in A'M'\) sao cho A’K = KG = GM’

Kẻ \(AH \bot A'M'\left( {H \in A'M'} \right) \Rightarrow AH \bot \left( {A'B'C'} \right) \Rightarrow A'H\)là hình chiếu vuông góc của AA’ trên (A’B’C’)

\( \Rightarrow \widehat {\left( {AA';\left( {A'B'C'} \right)} \right)} = \widehat {\left( {AA';AH} \right)} = \widehat {AA'H} = {60^0}\)

Ta có AHGI là hình chữ nhật nên

\(\begin{array}{l}AI = HG = \dfrac{1}{2}AM = \dfrac{1}{2}A'M';GM' = \dfrac{1}{3}A'M'\\ \Rightarrow A'H = A'M' - HG - GM' = A'M' - \dfrac{1}{2}A'M' - \dfrac{1}{3}A'M' = \dfrac{1}{6}A'M'\end{array}\)

Tam giác ABC đều cạnh a nên \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)

\(A'M' = \dfrac{{a\sqrt 3 }}{2} \Rightarrow A'H = \dfrac{1}{6}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{{12}}\)

Xét tam giác vuông AA’H có: \(AH = AA'.\tan 60 = \dfrac{{a\sqrt 3 }}{{12}}.\sqrt 3  = \dfrac{a}{4}\)

Vậy \({V_{ABC.A'B'C'}} = AA'.{S_{ABC}} = \dfrac{a}{4}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{{16}}\)

Đáp án cần chọn là: b