Cho khối lăng trụ tam giác $ABC.A'B'C'$ mà mặt bên $ABB'A'$ có diện tích bằng $4$. Khoảng cách giữa $CC'$ và mặt phẳng $\left( {ABB'A'} \right)$ bằng $7$. Thể tích khối lăng trụ là:
Phương pháp giải
- Dựng khối hộp từ lăng trụ tam giác đã cho.
- Tính thể tích khối hộp dựng được và suy ra thể tích khối lăng trụ tam giác cần tính.
Lời giải của Tự Học 365
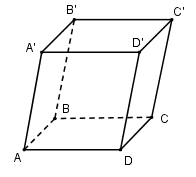
Dựng khối hộp $ABCD.A’B’C’D’$ ta có: \({V_{ABC.A'B'C'}} = \dfrac{1}{2}{V_{ABCD.A'B'C'D'}}\)
Khối hộp \(ABCD.A'B'C'D'\) có hai đáy là $ABB’A’$ và $CDD’C’$
\( \Rightarrow {V_{ABCD.A'B'C'D'}} = {S_{ABB'A'}}.h\)
Trong đó \(h = d\left( {\left( {ABB'A'} \right);\left( {CDD'C'} \right)} \right) = d\left( {CC';\left( {ABB'A'} \right)} \right) = 7\)
\( \Rightarrow {V_{ABCD.A'B'C'D'}} = 4.7 = 28\)
Vậy \({V_{ABC.A'B'C'}} = \dfrac{1}{2}.28 = 14\)
Đáp án cần chọn là: c
Toán Lớp 12
