Lời giải của Tự Học 365

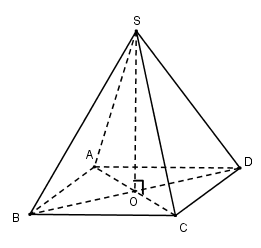
Gọi \(O = AC \cap BD\)

Vì chóp $S.ABCD$ đều nên \(SO \bot \left( {ABCD} \right)\)

Ta có: \(AC = BD = a\sqrt 2  \Rightarrow OA = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2}\)

\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OA \Rightarrow \Delta SOA\) vuông tại O \( \Rightarrow SO = \sqrt {S{A^2} - O{A^2}}  = \sqrt {{a^2} - \dfrac{{{a^2}}}{2}}  = \dfrac{{a\sqrt 2 }}{2}\)

Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}\dfrac{{a\sqrt 2 }}{2}{a^2} = \dfrac{{{a^3}\sqrt 2 }}{6}\)

Đáp án cần chọn là: a