Câu hỏi
Thông hiểu
Cho hình chóp \(S.ABC\) có \(SA \bot SB,SB \bot SC,SA \bot SC;SA = 2a,SB = b,SC = c\). Thể tích khối chóp là:
Đáp án đúng: a
Phương pháp giải
- Sử dụng công thức tính thể tích cho tứ diện vuông \(V = \dfrac{1}{6}abc\) để suy ra đáp án.
Lời giải của Tự Học 365
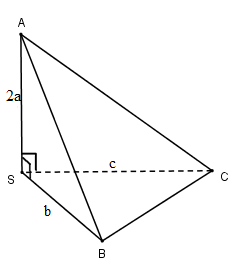
Ta có: \(\left. \begin{array}{l}SA \bot SB\\SA \bot SC\\SB \bot SC\end{array} \right\} \Rightarrow S.ABC\) là tứ diện vuông.
\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{6}SA.SB.SC = \dfrac{1}{6}.2a.b.c = \dfrac{1}{3}abc\).
Đáp án cần chọn là: a
Toán Lớp 12
