Câu hỏi
Nhận biết
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a.\) Diện tích xung quanh của hình trụ có đáy là hai hình tròn ngoại tiếp hai hình vuông \(ABCD\) và \(A'B'C'D'\) là:
Đáp án đúng: a
Phương pháp giải
Công thức tính diện tích xung quanh hình trụ có bán kính đáy \(R,\;\)chiều cao \(h:\;\;{S_{xq}} = 2\pi Rh.\)
Lời giải của Tự Học 365
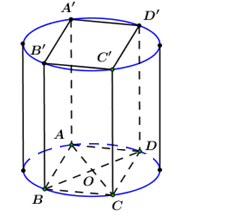
Ta có hình hộp \(ABCD.A'B'C'D'\) có các cạnh bằng \(a\)
\( \Rightarrow AA' = a\) là đường sinh của hình trụ.
Bán kính đáy của hình trụ là \(R = \dfrac{{AC}}{2} = \dfrac{{a\sqrt 2 }}{2}.\)
\( \Rightarrow \) Diện tích xung quanh của hình trụ là:
\({S_{xq}} = 2\pi Rl = 2\pi .\dfrac{{a\sqrt 2 }}{2}.a = \sqrt 2 \pi {a^2}.\)
Đáp án cần chọn là: a
Toán Lớp 12
