Lời giải của Tự Học 365

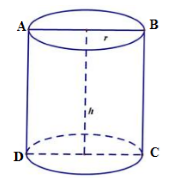
Gọi bán kính đáy và chiều cao của hình trụ lần lượt là \(r\) và \(h\left( {r,h > 0} \right)\)

Thiết diện là hình chữ nhật \(ABCD\) có chu vi \(2\left( {AB + BC} \right) = 2.\left( {h + 2r} \right)\)

Theo giả thiết ta có \(2\left( {h + 2r} \right) = 12 \Leftrightarrow h + 2r = 6 \Rightarrow h = 6 - 2r\,\,\left( {r < 3} \right)\)

Thể tích khối trụ \(V = \pi {r^2}h = \pi {r^2}.\left( {6 - 2r} \right) = \pi r.r.\left( {6 - 2r} \right)\)

Áp dụng BĐT Cô-si cho 3 số \(r;r;6 - 2r\) ta được

\(r + r + 6 - 2r \ge 3\sqrt[3]{{r.r\left( {6 - 2r} \right)}} \Leftrightarrow \sqrt[3]{{r.r\left( {6 - 2r} \right)}} \le 2 \Leftrightarrow {r^2}\left( {6 - 2r} \right) \le 8 \Leftrightarrow \pi {r^2}\left( {6 - 2r} \right) \le 8\pi \)

Hay \(V \le 8\pi \) . Dấu = xảy ra khi \(r = 6 - 2r \Leftrightarrow r = 2\left( {TM} \right)\)

Vậy giá trị lớn nhất của khối trụ là \(V = 8\pi .\) 

Đáp án cần chọn là: c