Lập phương trình chính tắc của hypebol $(H)$ biết $(H)$ có đỉnh ${A_2}(3;0)$ và đường tròn ngoại tiếp hình chữ nhật cơ sở là: $(C):\,{x^2} + {y^2} = 16$
Phương pháp giải
Hyberbol \(\left( H \right):\,\,\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1\) có đỉnh \({A_2}\left( {a;0} \right) \Rightarrow \) giá trị hệ số $a.$
Hình chữ nhật cơ sở có kích thước \(2a \times 2b \Rightarrow \) bán kính đường tròn ngoại tiếp hình chữ nhật cơ sở.
Lời giải của Tự Học 365
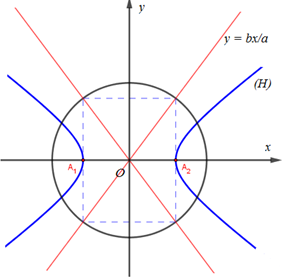
Gọi phương trình chính tắc của hypebol $(H)$ là: $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1,\,\,(a,\,b > 0)$
$(H)$ có đỉnh ${A_2}(3;0)$$ \Rightarrow a = 3$
Đường tròn $(C):\,{x^2} + {y^2} = 16$ có bán kính $R = 4$
$ \Rightarrow {a^2} + {b^2} = {4^2} \Rightarrow c = 4$
Mà ${a^2} + {b^2} = {c^2} \Rightarrow {3^2} + {b^2} = {4^2} \Leftrightarrow {b^2} = 7$
Phương trình chính tắc của $(H):$ $\dfrac{{{x^2}}}{9} - \dfrac{{{y^2}}}{7} = 1$
Đáp án cần chọn là: a
Toán Lớp 12
