Cho hình lăng trụ \(ABC.A'B'C'\). Gọi \(H\) là trung điểm của \(A'B'\). Đường thẳng \(B'C\) song song với mặt phẳng nào sau đây?
Phương pháp giải
- Gọi \(K = BC' \cap B'C\) và \(I\) là trung điểm của \(AB\).
- Chứng minh \(\left( {IB'C} \right)//\left( {AHC'} \right)\) dựa vào dấu hiệu: \(\left\{ \begin{array}{l}a//\left( P \right)\\b//\left( P \right)\\a \cap b = I\end{array} \right. \Rightarrow \left( {a,b} \right)//\left( P \right)\)
Lời giải của Tự Học 365
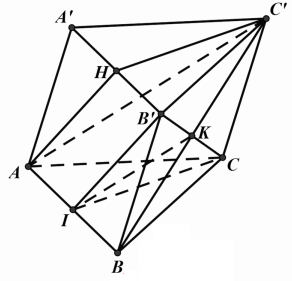
Gọi \(K = BC' \cap B'C\) và \(I\) là trung điểm của \(AB\).
Khi đó \(AHB'I\) là hình bình hành \(\left( {AI//HB',AI = HB'} \right)\).
Suy ra \(AH//B'I\).
Mặt khác, xét tam giác \(ABC'\) có \(IK\) là đường trung bình của tam giác nên \(IK//AC'\).
Do đó \(\left\{ \begin{array}{l}IB'//AH\\IK//AC'\\IB',IK \subset \left( {IB'C} \right)\\AH,AC' \subset \left( {AHC'} \right)\end{array} \right. \Rightarrow \left( {IB'C} \right)//\left( {AHC'} \right) \Rightarrow B'C//\left( {AHC'} \right)\)
Đáp án cần chọn là: a
Toán Lớp 12
