Lời giải của Tự Học 365

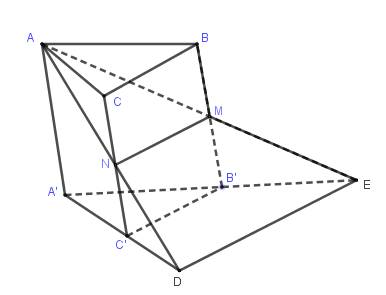
Gọi \(D = AN \cap A'C' \Rightarrow D \in \left( {AMN} \right) \cap \left( {A'B'C'} \right)\) và \(E = AM \cap A'B' \Rightarrow E \in \left( {AMN} \right) \cap \left( {A'B'C'} \right)\).

Khi đó \(DE = \left( {AMN} \right) \cap \left( {A'B'C'} \right) = \Delta \).

Lại có: \(\left\{ \begin{array}{l}\left( {AMN} \right) \cap \left( {MNC'B'} \right) = MN\\\left( {A'B'C'} \right) \cap \left( {MNC'B'} \right) = B'C'\\\left( {AMN} \right) \cap \left( {A'B'C'} \right) = DE\\MN//B'C'\end{array} \right. \Rightarrow MN//B'C'//DE\) (định lý ba giao tuyến)

Do đó \(DE//B'C'//BC\).

Đáp án cần chọn là: c