Cho hình hộp \(ABCD.A'B'C'D'\), mặt phẳng \(\left( \alpha \right)\) qua \(AB\) và trung điểm \(M\) của \(CC'\) thì cắt hình hộp theo thiết diện là hình gì?
Phương pháp giải
- Xác định thiết diện của hình hộp khi cắt bởi mặt phẳng \(\left( \alpha \right)\).
- Sử dụng các tính chất song song của đường thẳng, mặt phẳng để tìm hình dạng của thiết diện.
Lời giải của Tự Học 365
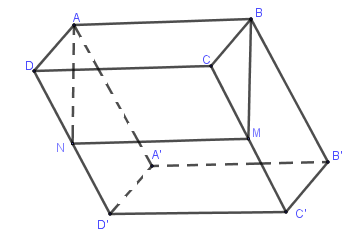
Ta sử dụng tính chất: Nếu một mặt phẳng cắt một trong hai mặt phẳng song song thì nó sẽ cắt mặt phẳng còn lại và giao tuyến của chúng song song.
Ta có:
\(\left. \begin{array}{l}\left( {ADD'A'} \right)//\left( {BCC'B'} \right)\\\left( {ABM} \right) \cap \left( {BCC'B'} \right) = BM\end{array} \right\} \Rightarrow \left( {ABM} \right) \cap \left( {ADD'A'} \right) = AN//BM\) với \(N \in DD'\).
Do đó tứ giác \(ABMN\) là hình thang.
Lại có:
\(\left. \begin{array}{l}\left( {ABB'A'} \right)//\left( {DCC'D'} \right)\\\left( {ABMN} \right) \cap \left( {ABB'A'} \right) = AB\\\left( {ABMN} \right) \cap \left( {DCC'D'} \right) = MN\end{array} \right\} \Rightarrow AB//MN\)
Do đó tứ giác \(ABMN\) là hình bình hành.
Đáp án cần chọn là: c
Toán Lớp 12
