Câu hỏi
Nhận biết
Cho hình hộp $ABCD.A'B'C'D'$. Mặt phẳng $\left( {AB'D'} \right)$ song song với mặt phẳng nào trong các mặt phẳng sau đây?
Đáp án đúng: b
Phương pháp giải
- Bước 1: Chứng minh mặt phẳng \(\left( \alpha \right)\) chứa hai đường thẳng \(a,b\) cắt nhau lần lượt song song với hai đường thẳng \(a',b'\) cắt nhau trong mặt phẳng \(\left( \beta \right)\).
- Bước 2: Kết luận \(\left( \alpha \right)//\left( \beta \right)\).
Lời giải của Tự Học 365
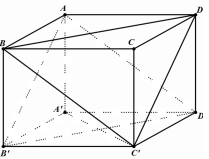
Do \(ADC'B'\) là hình bình hành nên \(AB'//DC'\).
Do \(ABC'D'\) là hình bình hành nên \(AD'//BC'\).
Mà \(AB',AD' \subset \left( {AB'D'} \right);BC',DC' \subset \left( {BC'D} \right)\) nên \(\left( {AB'D'} \right)//\left( {BC'D} \right)\).
Đáp án cần chọn là: b
Toán Lớp 12
