Câu hỏi
Thông hiểu
Cho hình bình hành \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Gọi \(E,\;F\) lần lượt là trung điểm của \(AB,\;BC\). Đẳng thức nào sau đây sai?
Đáp án đúng: d
Phương pháp giải
Dựng hình, nhận xét tính đúng sai của các đáp án và kết luận.
Lời giải của Tự Học 365
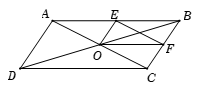
Ta có \(OF,\;OE\) lần lượt là đường trung bình của tam giác \(\Delta BCD\) và \(\Delta ABC\).
\( \Rightarrow BEOF\) là hình bình hành.
\(\overrightarrow {BE} + \overrightarrow {BF} = \overrightarrow {BO} \)\( \Rightarrow \overrightarrow {BE} + \overrightarrow {BF} - \overrightarrow {DO} = \overrightarrow {BO} - \overrightarrow {DO} \) \( = \overrightarrow {OD} - \overrightarrow {OB} = \overrightarrow {BD} \)
Đáp án cần chọn là: d
Toán Lớp 12
