Lời giải của Tự Học 365

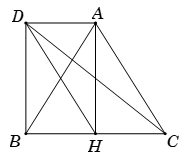
Gọi \(D\) là điểm thỏa mãn tứ giác \(ACHD\) để ACHD là hình bình hành

\( \Rightarrow AHBD\) là hình chữ nhật.

\(\left| {\overrightarrow {CA}  - \overrightarrow {HC} } \right| = \left| {\overrightarrow {CA}  + \overrightarrow {CH} } \right| = \left| {\overrightarrow {CD} } \right| = CD.\)

Ta có \(CD = \sqrt {B{D^2} + B{C^2}}  = \sqrt {A{H^2} + B{C^2}} \)\( = \sqrt {\dfrac{{3{a^2}}}{4} + {a^2}}  = \dfrac{{a\sqrt 7 }}{2}\)

Đáp án cần chọn là: d