. Giả sử \(CD = h\) là chiều cao của tháp trong đó \(C\) là chân tháp. Chọn hai điểm \(A,{\rm{ }}B\) trên mặt đất sao cho ba điểm \(A,{\rm{ }}B\) và \(C\) thẳng hàng. Ta đo được \(AB = 24{\rm{ m}}\), \(\widehat {CAD} = {63^0},{\rm{ }}\widehat {CBD} = {48^0}\).
Chiều cao \(h\) của tháp gần với giá trị nào sau đây?
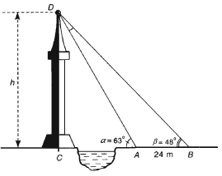
Phương pháp giải
Giải tam giác \(ACD\) rồi kết luận
Lời giải của Tự Học 365
Áp dụng định lí sin vào tam giác \(ABD,\) ta có \(\dfrac{{AD}}{{\sin \beta }} = \dfrac{{AB}}{{\sin D}}.\)
Ta có \(\alpha = \widehat D + \beta \) nên \(\widehat D = \alpha - \beta = {63^0} - {48^0} = {15^0}.\)
Do đó \(AD = \dfrac{{AB.\sin \beta }}{{\sin \left( {\alpha - \beta } \right)}} = \dfrac{{24.\sin {{48}^0}}}{{\sin {{15}^0}}} \approx 68,91{\rm{ m}}.\)
Trong tam giác vuông \(ACD,\) có \(h = CD = AD.\sin \alpha \approx 61,4{\rm{ m}}.\)
Đáp án cần chọn là: d
Toán Lớp 12
