Câu hỏi
Vận dụng
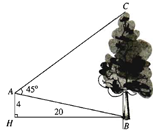
Từ vị trí \(A\) người ta quan sát một cây cao (hình vẽ).
Đáp án đúng: b
Phương pháp giải
Giải tam giác \(ABC\) và kết luận.
Lời giải của Tự Học 365
Trong tam giác \(AHB\), ta có \(\tan \widehat {ABH} = \dfrac{{AH}}{{BH}} = \dfrac{4}{{20}} = \dfrac{1}{5}\) \( \Rightarrow \widehat {ABH} \approx {11^0}19\)
Suy ra \(\widehat {ABC} = {90^0} - \widehat {ABH} = {78^0}41'\).
Suy ra \(\widehat {ACB} = {180^0} - \left( {\widehat {BAC} + \widehat {ABC}} \right) = {56^0}19'\).
Áp dụng định lý sin trong tam giác \(ABC\), ta được \(\dfrac{{AB}}{{\sin \widehat {ACB}}} = \dfrac{{CB}}{{\sin \widehat {BAC}}}\)\( \Rightarrow CB = \dfrac{{AB.\sin \widehat {BAC}}}{{\sin \widehat {ACB}}} \approx 17{\rm{m}}\)
Đáp án cần chọn là: b
Toán Lớp 12
