Hai chiếc tàu thủy cùng xuất phát từ một vị trí \(A\), đi thẳng theo hai hướng tạo với nhau góc \({60^0}\). Tàu \(B\) chạy với tốc độ \(20\) hải lí một giờ. Tàu \(C\) chạy với tốc độ \(15\) hải lí một giờ. Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí? Kết quả gần nhất với số nào sau đây?
Phương pháp giải
- Tính độ dài các đoạn \(AB,AC\).
- Sử dụng định lý hàm số cô sin cho tam giác \(ABC\) và kết luận
Lời giải của Tự Học 365
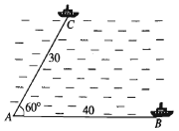
Sau \(2\) giờ tàu \(B\) đi được \(40\) hải lí, tàu \(C\) đi được \(30\) hải lí. Vậy tam giác \(ABC\) có \(AB = 40,\,\,\,AC = 30\) và \(\widehat A = {60^0}.\)
Áp dụng định lí côsin vào tam giác \(ABC,\) ta có
\({a^2} = {b^2} + {c^2} - 2bc\cos A\)\( = {30^2} + {40^2} - 2.30.40.\cos {60^0}\)\( = 900 + 1600 - 1200 = 1300\)
Vậy \(BC = \sqrt {1300} \approx 36\) (hải lí).
Sau \(2\) giờ, hai tàu cách nhau khoảng \(36\) hải lí.
Đáp án cần chọn là: b
Toán Lớp 12
