Cho góc \(\widehat {xOy} = 30^\circ \). Gọi \(A\) và \(B\) là hai điểm di động lần lượt trên \(Ox\) và \(Oy\) sao cho \(AB = 1\). Khi \(OB\) có độ dài lớn nhất thì độ dài của đoạn \(OA\) bằng:
Phương pháp giải
Sử dụng định lý hàm số sin cho tam giác \(OAB\) và đánh giá GTLN của \(OB\), từ đó suy ra độ dài của \(OA\).
Lời giải của Tự Học 365
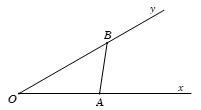
Theo định lí hàm sin, ta có
\(\dfrac{{OB}}{{\sin \widehat {OAB}}} = \dfrac{{AB}}{{\sin \widehat {AOB}}}\)\( \Leftrightarrow OB = \dfrac{{AB}}{{\sin \widehat {AOB}}}.\sin \widehat {OAB}\) \( = \dfrac{1}{{\sin 30^\circ }}.\sin \widehat {OAB} = 2\sin \widehat {OAB}\)
Do đó, độ dài \(OB\) lớn nhất khi và chỉ khi \(\sin \widehat {OAB} = 1 \Leftrightarrow \widehat {OAB} = 90^\circ \).
Khi đó \(OB = 2\).
Tam giác \(OAB\) vuông tại \(A\)\( \Rightarrow OA = \sqrt {O{B^2} - A{B^2}} = \sqrt {{2^2} - {1^2}} = \sqrt 3 \)
Đáp án cần chọn là: b
Toán Lớp 12
