Lời giải của Tự Học 365

Trừ phương trình 1 cho 2 vế với vế ta được:

\({2^x} - {2^y} = 2y - 2x \Leftrightarrow {2^x} + 2x = {2^y} + 2y\)

Xét hàm \(f\left( t \right) = {2^t} + 2t\) có \(f'\left( t \right) = {2^t}\ln 2 + 2 > 0,\forall t \in R\) nên hàm số \(f\left( t \right)\) đồng biến trên \(R\).

Do đó \(f\left( x \right) = f\left( y \right) \Leftrightarrow x = y\).

Thay \(y = x\) vào phương trình \({2^x} = 2y\) ta được \({2^x} = 2x \Leftrightarrow {2^x} - 2x = 0\).

Xét hàm \(y=g\left( x \right) = {2^x} - 2x\) có \(g'\left( x \right) = {2^x}\ln 2 - 2 = 0 \Leftrightarrow x = {\log _2}\dfrac{2}{{\ln 2}}\).

Suy ra \(g'\left( x \right) > 0 \Leftrightarrow x > {\log _2}\dfrac{2}{{\ln 2}};\) \(g'\left( x \right) < 0 \Leftrightarrow x < {\log _2}\dfrac{2}{{\ln 2}}\)

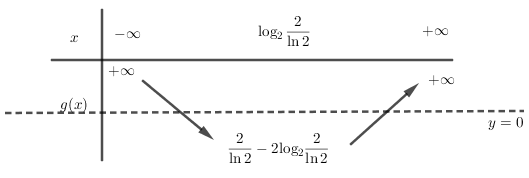
\( \Rightarrow x = {\log _2}\dfrac{2}{{\ln 2}}\) là điểm cực tiểu của hàm số\( \Rightarrow {y_{CT}} = {2^{{{\log }_2}\frac{2}{{\ln 2}}}} - 2{\log _2}\dfrac{2}{{\ln 2}} = \dfrac{2}{{\ln 2}} - 2{\log _2}\dfrac{2}{{\ln 2}} < 0\)

Mặt khác \(\mathop {\lim }\limits_{x \to  \pm \infty } g(x) =  + \infty \) suy ra đường thẳng \(y = 0\) cắt đồ thị hàm số \(y = g\left( x \right)\) tại \(2\) điểm phân biệt.

Vậy số nghiệm của hệ là \(2\)

Đáp án cần chọn là: a