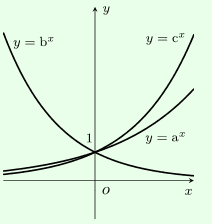
Cho các đồ thị hàm số \(y = {a^x},y = {b^x},y = {c^x}\left( {0 < a,b,c e 1} \right)\), chọn khẳng định đúng:
Phương pháp giải
- Bước 1: Quan sát các đồ thị, nhận xét về tính đơn điệu để nhận xét các cơ số.
+ Hàm số đồng biến thì cơ số lớn hơn \(1\).
+ Hàm số nghịch biến thì cơ số lớn hơn \(0\) và nhỏ hơn \(1\).
- Bước 2: So sánh các cơ số dựa vào phần đồ thị của hàm số.
- Bước 3: Kết hợp các điều kiện ở trên ta được mối quan hệ cần tìm.
Lời giải của Tự Học 365
Ta thấy:
- Hàm số \(y = {b^x}\) nghịch biến nên \(0 < b < 1\).
- Hàm số \(y = {a^x},y = {c^x}\) đồng biến nên \(a,c > 1 > b\), loại B và D.
- Xét phần đồ thị hai hàm số \(y = {a^x},y = {c^x}\) ta thấy phần đồ thị hàm số \(y = {c^x}\) nằm trên đồ thị hàm số \(y = {a^x}\) nên \({c^x} > {a^x},\forall x > 0 \Leftrightarrow c > a\).
Đáp án cần chọn là: a
Toán Lớp 12
