Câu hỏi
Vận dụng
Cho $a$ là số thực tùy ý và $b,{\rm{ }}c$ là các số thực dương khác $1$. Hình vẽ bên là đồ thị của ba hàm số $G$, $A\left( {1; - 1; - 2} \right)$ và $y = {x^a},{\rm{ }}x > 0$. Khẳng định nào sau đây là đúng?
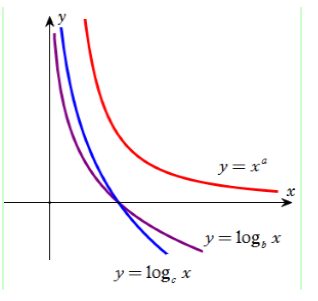
Đáp án đúng: b
Phương pháp giải
Nhận xét \(a,b,c\) dựa vào đồ thị các hàm số đã cho.
Lời giải của Tự Học 365
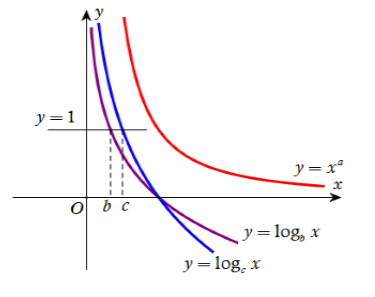
Nhận thấy hàm số $y = {x^a}$ nghịch biến \( \Rightarrow a < 0.\) Do đó ta loại ngay đáp án C và D (vì $b,{\rm{ }}c$ là các số thực dương khác $1$).
Kẻ đường thẳng \(y = 1\) cắt đồ thị của hai hàm số $G$, $A\left( {1; - 1; - 2} \right)$ lần lượt tại điểm có hoành độ là \(x = b\) và \(x = c\) như hình vẽ. Dựa vào hình vẽ ta thấy \(0 < b < c.\)
Vậy \(a < b < c.\)
Đáp án cần chọn là: b
Toán Lớp 12
