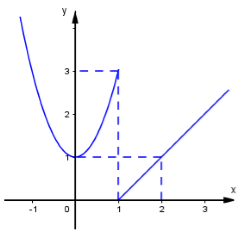
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ, chọn kết luận đúng:
Phương pháp giải
Hàm số liên tục trên một khoảng nếu nó liên tục tại mọi điểm thuộc khoảng đó.
Lời giải của Tự Học 365
Quan sát đồ thị ta thấy \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = 3;\,\,\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = 0 \Rightarrow \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) e \mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right)\) nên không tồn tại \(\mathop {\lim }\limits_{x \to {1^{}}} f\left( x \right)\). Do đó hàm số gián đoạn tại điểm x = 1.
Do đó hàm số không liên tục trên mọi khoảng có chứa điểm \(x = 1\) hay A, B sai, D đúng.
Đáp án C sai do hàm số liên tục trên khoảng \(\left( { - \infty ;0} \right)\).
Đáp án cần chọn là: d
Toán Lớp 12
