Câu hỏi
Nhận biết
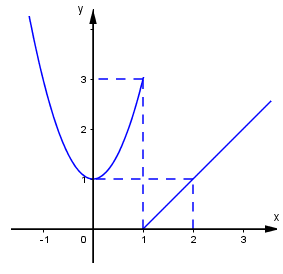
Hàm số \(y = f\left( x \right)\) có đồ thị dưới đây gián đoạn tại điểm có hoành độ bằng bao nhiêu?
Đáp án đúng: b
Phương pháp giải
Hàm số \(y = f\left( x \right)\) liên tục tại điểm \(x = {x_0}\) khi và chỉ khi \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Lời giải của Tự Học 365
Quan sát đồ thị ta thấy \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = 3;\,\,\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = 0 \) \(\Rightarrow \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) e \mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right)\) nên không tồn tại \(\mathop {\lim }\limits_{x \to {1^{}}} f\left( x \right)\). Do đó hàm số gián đoạn tại điểm $x = 1.$
Đáp án cần chọn là: b
Toán Lớp 12
