Câu hỏi
Vận dụng
Cho hàm số \(y = - {x^2} + 2x + 1.\) Gọi $M$ và $m$ là giá trị lớn nhất vá giá trị nhỏ nhất của hàm số trên \(\left[ {0;2} \right]\). Tính giá trị của biểu thức \(T = {M^2} + {m^2}.\)
Đáp án đúng: a
Phương pháp giải
Lập BBT của hàm số trên một đoạn để tìm GTLN và GTNN của hàm số trên đoạn đó.
Lời giải của Tự Học 365
Hàm số \(y = - {x^2} + 2x + 1\) có \(a = - 1 < 0\,;\,\, - \dfrac{b}{{2a}} = 1 \Rightarrow \) Hàm số đồng biến trên \(\left( { - \infty ;1} \right)\) và nghịch biến trên \(\left( {1; + \infty } \right)\).
BBT:
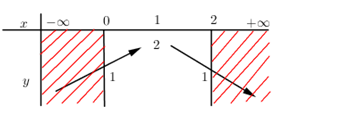
Dựa vào BBT ta thấy $M = 2$ và $m = 1$ \( \Rightarrow T = {M^2} + {m^2} = {2^2} + {1^2} = 5.\)
Đáp án cần chọn là: a
Toán Lớp 12
