Bảng biến thiên của hàm số $y = –x^2+ 2x – 1$ là:
Phương pháp giải
- Parabol \(y = a{x^2} + bx + c\,\,\left( {a e 0} \right)\) có tọa độ đỉnh là \(\left( { - \dfrac{b}{{2a}}; - \dfrac{\Delta }{{4a}}} \right).\)
- Nếu $a > 0$ thì hàm số tăng (đồng biến) trên \(\left( { - \dfrac{b}{{2a}}; + \infty } \right)\) và giảm (nghịch biến) trên \(\left( { - \infty ; - \dfrac{b}{{2a}}} \right)\).
- Nếu $a < 0$ thì hàm số tăng (đồng biến) trên \(\left( { - \infty ; - \dfrac{b}{{2a}}} \right)\) và giảm (nghịch biến) trên \(\left( { - \dfrac{b}{{2a}}; + \infty } \right)\).
Lời giải của Tự Học 365
Ta có:
\(\begin{array}{l}a = - 1 < 0\,\,;\,\,\dfrac{{ - b}}{{2a}} = \dfrac{{ - 2}}{{2.( - 1)}} = \dfrac{{ - 2}}{{ - 2}} = 1\\y(1) = - {1^2} + 2.1 - 1 = 0.\end{array}\)
Suy ra bảng biến thiên:
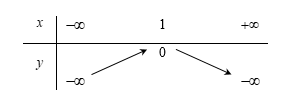
Đáp án cần chọn là: c
Toán Lớp 12
