Cho hình chóp S.ABCD có đáy ABCD là hình thang có các đáy AD và BC. Gọi M là trọng tâm tam giác SAD, N là điểm thuộc AC sao cho \(NA = \dfrac{{NC}}{2}\), P là điểm thuộc đoạn CD sao cho \(PD = \dfrac{{PC}}{2}\) . Khi đó mệnh đề nào sau đây là đúng?
Phương pháp giải
Dựa vào phương pháp chứng minh hai mặt phẳng song song: Hai đường thẳng cắt nhau trong mặt phẳng này lần lượt song song với hai đường thẳng trong mặt phẳng kia thì hai mặt phẳng đó song song và tính chất: Nếu hai mặt phẳng song song thì mọi đường thẳng nằm trong mặt phẳng này song song với mặt phẳng kia.
Lời giải của Tự Học 365
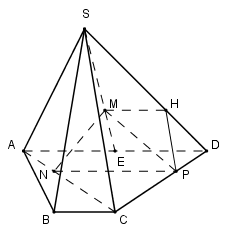
Gọi \(H \in SD\) sao cho \(HD = \dfrac{1}{2}SH\)
Ta có: \(\dfrac{{SM}}{{SE}} = \dfrac{{SH}}{{SD}} = \dfrac{2}{3} \Rightarrow MH//AD//NP \Rightarrow M,H,P,N\) đồng phẳng.
Ta có:
\(\begin{array}{l}\dfrac{{AN}}{{AC}} = \dfrac{{DP}}{{DC}} = \dfrac{1}{3} \Rightarrow NP//AD;\,\,\dfrac{{DH}}{{DS}} = \dfrac{{DP}}{{DC}} = \dfrac{1}{3} \Rightarrow HP//SC\\\left\{ \begin{array}{l}NP//AD//BC\\HP//SC\end{array} \right. \Rightarrow \left( {MHPN} \right)//\left( {SBC} \right) \Rightarrow \left( {MNP} \right)//\left( {SBC} \right)\\MN \subset \left( {MNP} \right) \Rightarrow MN//\left( {SBC} \right)\end{array}\)
Đáp án cần chọn là: a
Toán Lớp 12
