Cho hình lập phương $ABCD.EFGH$ có cạnh bằng $a$ . Tính \(\overrightarrow {AB} .\overrightarrow {EG} .\)
Phương pháp giải
Biểu diễn véc tơ \(\overrightarrow {EG} \) qua các véc tơ không đồng phẳng có giá là các cạnh của hình lập phương, từ đó tính tích vô hướng.
Lời giải của Tự Học 365
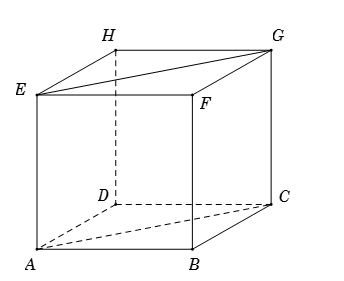
Ta có \(\overrightarrow {AB} .\overrightarrow {EG} = \overrightarrow {AB} .\overrightarrow {AC} .\) Mặt khác \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \).
Suy ra \(\overrightarrow {AB} .\overrightarrow {EG} = \overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AB} \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) = {\overrightarrow {AB} ^2} + \overrightarrow {AB} .\overrightarrow {AD} \).
Vì \(ABCD\) là hình vuông \( \Rightarrow AB \bot AD \Leftrightarrow \overrightarrow {AB} .\overrightarrow {AD} = 0\)
\( \Rightarrow {\overrightarrow {AB} ^2} + \overrightarrow {AB} .\overrightarrow {AD} = A{B^2} + 0 = {a^2}.\)
Đáp án cần chọn là: b
Toán Lớp 12
