Lời giải của Tự Học 365

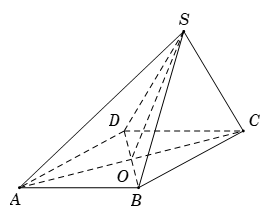
Theo giả thiết, ta có \(AB = BC = CD = DA = a\) nên \(ABCD\) là hình thoi cạnh \(a\).

Gọi \(O = AC \cap BD\). Ta có \(\Delta CBD = \Delta SBD{\rm{ }}\left( {c - c - c} \right)\).

Suy ra hai đường trung tuyến tương ứng \(CO\) và \(SO\) bằng nhau.

Xét tam giác \(SAC\), ta có \(SO = CO = \dfrac{1}{2}AC\).

Do đó tam giác \(SAC\) vuông tại \(S\) (tam giác có đường trung tuyến bằng nửa cạnh đáy).

Vậy \(SA \bot SC\).

Đáp án cần chọn là: d