Câu hỏi
Vận dụng
Cho hình lập phương \(ABCD.A'B'C'D'\). Góc giữa $AC$ và $DA'$ là:
Đáp án đúng: c
Phương pháp giải
Sử dụng mối quan hệ song song giữa các đường thẳng và kiến thức hình học đã biết để xác định góc giữa hai đường thẳng bài yêu cầu.
Lời giải của Tự Học 365
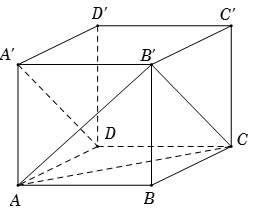
Gọi \(a\) là độ dài cạnh hình lập phương. Khi đó, tam giác \(AB'C\) đều (\(AB' = B'C = CA = a\sqrt 2 \)) do đó \(\widehat {B'CA} = {60^0}\).
Lại có, \(DA'\) song song \(CB'\) nên \(\left( {AC,DA'} \right) = \left( {AC,CB'} \right) = \widehat {ACB'} = {60^0}.\)
Đáp án cần chọn là: c
Toán Lớp 12
