Lời giải của Tự Học 365

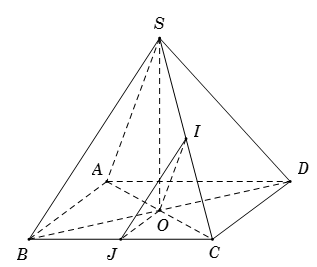
Gọi \(O\) là tâm của hình thoi \(ABCD \Rightarrow \)\(OJ\) là đường trung bình của \(\Delta BCD.\)

Suy ra \(\left\{ \begin{array}{l}OJ\,\parallel \,CD\\OJ = \dfrac{1}{2}CD\end{array} \right.\).

Vì \(CD\,\parallel \,OJ \Rightarrow \left( {IJ,CD} \right) = \left( {IJ,OJ} \right)\).

Xét tam giác $IOJ$, có \(\left\{ \begin{array}{l}IJ = \dfrac{1}{2}SB = \dfrac{a}{2}\\OJ = \dfrac{1}{2}CD = \dfrac{a}{2}\\IO = \dfrac{1}{2}SA = \dfrac{a}{2}\end{array} \right.\) $ \Rightarrow \Delta IOJ$ đều.

Vậy \(\left( {IJ,CD} \right) = \left( {IJ,OJ} \right) = \widehat {IJO} = 60^\circ \).

Đáp án cần chọn là: d