Lời giải của Tự Học 365

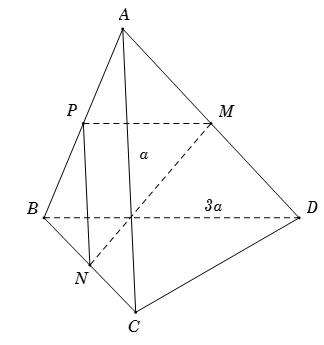
Gọi \(P\) là trung điểm của \(AB\) \( \Rightarrow PN,PM\) lần lượt là đường trung bình của tam giác \(\Delta ABC\) và \(\Delta ABD\). Suy ra \(\left\{ \begin{array}{l}PN = \dfrac{1}{2}AC = \dfrac{a}{2}\\PM = \dfrac{1}{2}BD = \dfrac{{3a}}{2}\end{array} \right..\)

Ta có \(AC \bot BD \Rightarrow PN \bot PM\) hay tam giác \(\Delta PMN\) vuông tại \(P\)

Do đó \(MN = \sqrt {P{N^2} + P{M^2}}  = \sqrt {\dfrac{{{a^2}}}{4} + \dfrac{{9{a^2}}}{4}}  = \dfrac{{a\sqrt {10} }}{2}.\)

Đáp án cần chọn là: b