Cho tứ diện$ABCD$ có $AB = AC = AD$ và \(\widehat {BAC} = \widehat {BAD} = {60^0}\). Gọi $I$ và $J$ lần lượt là trung điểm của $AB$ và $CD$. Hãy xác định góc giữa cặp vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {IJ} \)?
Phương pháp giải
- Biểu diễn véc tơ \(\overrightarrow {IJ} \) qua hai véc tơ \(\overrightarrow {IC} ,\overrightarrow {ID} \).
- Sử dụng công thức tích vô hướng để tính góc giưa hai véc tơ.
Lời giải của Tự Học 365
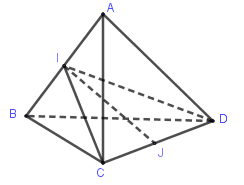
Xét tam giác\(ICD\) có \(J\) là trung điểm đoạn \(CD\).
Ta có: \(\overrightarrow {IJ} = \dfrac{1}{2}\left( {\overrightarrow {IC} + \overrightarrow {ID} } \right)\)
Vì tam giác \(ABC\) có \(AB = AC\) và \(\widehat {BAC} = 60^\circ \)
Nên tam giác \(ABC\)đều. Suy ra: \(CI \bot AB\)
Tương tự ta có tam giác \(ABD\) đều nên \(DI \bot AB\).
Xét \(\overrightarrow {IJ} .\overrightarrow {AB} = \dfrac{1}{2}\left( {\overrightarrow {IC} + \overrightarrow {ID} } \right).\overrightarrow {AB} = \dfrac{1}{2}\overrightarrow {IC} .\overrightarrow {AB} + \dfrac{1}{2}\overrightarrow {ID} .\overrightarrow {AB} = \overrightarrow 0 \).
Suy ra \(\overrightarrow {IJ} \bot \overrightarrow {AB} \). Hay góc giữa cặp vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {IJ} \) bằng \({90^0}\).
Đáp án cần chọn là: b
Toán Lớp 12
