Trong không gian cho hai tam giác đều $ABC$ và $ABC'$ có chung cạnh $AB$ và nằm trong hai mặt phẳng khác nhau. Gọi $M,{\rm{ }}N,{\rm{ }}P,{\rm{ }}Q$ lần lượt là trung điểm của các cạnh $AC,{\rm{ }}CB,{\rm{ }}BC'$ và $C'A$ . Tứ giác $MNPQ$ là hình gì?
Phương pháp giải
Dựng hình, nhận xét tính chất của tứ giác dựa vào các mối quan hệ song song, vuông góc của các đường thẳng.
Lời giải của Tự Học 365
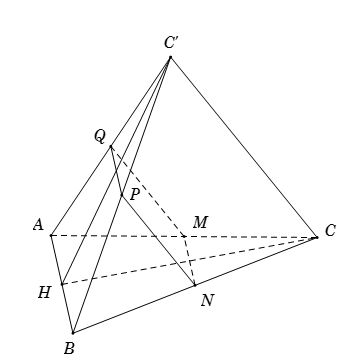
Vì $M,{\rm{ }}N,{\rm{ }}P,{\rm{ }}Q$ lần lượt là trung điểm của các cạnh $AC,{\rm{ }}CB,{\rm{ }}BC'$ và $C'A$
\( \Rightarrow \left\{ \begin{array}{l}PQ = MN = \dfrac{1}{2}AB\\PQ//AB//MN\end{array} \right.\)\( \Rightarrow \) \(MNPQ\) là hình bình hành.
Gọi \(H\) là trung điểm của \(AB\). Vì hai tam giác $ABC$ và $ABC'$ đều nên \(\left\{ \begin{array}{l}CH \bot AB\\C'H \bot AB\end{array} \right..\)
Suy ra \(AB \bot \left( {CHC'} \right)\). Do đó \(AB \bot CC'\).
Ta có \(\left\{ \begin{array}{l}PQ{\rm{//}}AB\\PN{\rm{//}}CC'\\AB \bot CC'\end{array} \right. \Rightarrow PQ \bot PN\) .
Vậy tứ giác $MNPQ$là hình chữ nhật.
Đáp án cần chọn là: b
Toán Lớp 12
