Cho hình lập phương $ABCD.EFGH$. Hãy xác định góc giữa cặp vectơ \(\overrightarrow {AF} \) và \(\overrightarrow {EG} \)?
Phương pháp giải
- Biểu diễn các véc tơ \(\overrightarrow {AF} ,\overrightarrow {EG} \) qua ba véc tơ \(\overrightarrow {AB} ,\overrightarrow {AD} ,\overrightarrow {AE} \).
- Tính tích có hướng \(\overrightarrow {AF} .\overrightarrow {EG} \) rồi suy ra giá trị \(\cos \left( {\overrightarrow {AF} ,\overrightarrow {EG} } \right) = \dfrac{{\overrightarrow {AF} .\overrightarrow {EG} }}{{\left| {\overrightarrow {AF} } \right|.\left| {\overrightarrow {EG} } \right|}}\)
Lời giải của Tự Học 365
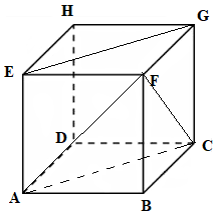
Ta có:
\(\begin{array}{l}\overrightarrow {AF} = \overrightarrow {AB} + \overrightarrow {AE} \\\overrightarrow {EG} = \overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \\ \Rightarrow \overrightarrow {AF} .\overrightarrow {EG} = \left( {\overrightarrow {AB} + \overrightarrow {AE} } \right).\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) = A{B^2} + \overrightarrow {AE} .\overrightarrow {AB} + \overrightarrow {AB} .\overrightarrow {AD} + \overrightarrow {AE} .\overrightarrow {AD} = A{B^2}\\ \Rightarrow \cos \left( {\overrightarrow {AF} ,\overrightarrow {EG} } \right) = \dfrac{{\overrightarrow {AF} .\overrightarrow {EG} }}{{\left| {\overrightarrow {AF} } \right|.\left| {\overrightarrow {EG} } \right|}} = \dfrac{{{a^2}}}{{a\sqrt 2 .a\sqrt 2 }} = \dfrac{1}{2} \Rightarrow \widehat {\left( {\overrightarrow {AF} ,\overrightarrow {EG} } \right)} = {60^0}\end{array}\)
Đáp án cần chọn là: b
Toán Lớp 12
