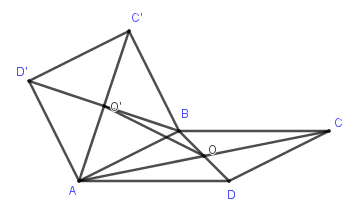
Trong không gian cho hai hình vuông $ABCD$ và $ABC'D'$ có chung cạnh $AB$ và nằm trong hai mặt phẳng khác nhau, lần lượt có tâm $O$ và $O'$. Hãy xác định góc giữa cặp vectơ \(\overrightarrow {AB} \) và $\overrightarrow {OO'} $?
Phương pháp giải
Tính tích vô hướng của hai véc tơ \(\overrightarrow {AB} \) và \(\overrightarrow {OO'} \).
Lời giải của Tự Học 365
Do \(O,O'\) là tâm các hình vuông \(ABCD,ABC'D'\) nên \(O,O'\) là trung điểm của \(BD,BD'\).
Do đó \(OO'\) là đường trung bình của tam giác \(BDD'\) \( \Rightarrow \overrightarrow {OO'} = \dfrac{1}{2}\overrightarrow {DD'} \)
Ta có:
\(\overrightarrow {AB} .\overrightarrow {OO'} = \overrightarrow {AB} .\dfrac{1}{2}\overrightarrow {DD'} = \dfrac{1}{2}.\overrightarrow {AB} \left( {\overrightarrow {AD'} - \overrightarrow {AD} } \right)\) \( = \dfrac{1}{2}\overrightarrow {AB} .\overrightarrow {AD'} - \dfrac{1}{2}\overrightarrow {AB} .\overrightarrow {AD} = 0 - 0 = 0\)
Do đó góc giữa \(\overrightarrow {AB} \) và \(\overrightarrow {OO'} \) bằng \({90^0}\)
Đáp án cần chọn là: d
Toán Lớp 12
