Lời giải của Tự Học 365

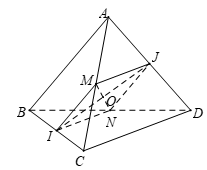
Gọi \(M\), \(N\) lần lượt là trung điểm \(AC\), \(BD.\)

Ta có:

\(\left\{ \begin{array}{l}MI = NI = \dfrac{1}{2}AB = \dfrac{1}{2}CD = \dfrac{a}{2}\\MI{\text{ // }}AB{\text{ // }}NJ,MJ//CD//IN\end{array} \right. \Rightarrow MINJ\) là hình thoi.

Gọi \(O\) là giao điểm của \(MN\) và \(IJ\).

Ta có: \(\widehat {MIN} = 2\widehat {MIO}\).

Xét \(\Delta MIO\) vuông tại \(O\), ta có: \(\cos \widehat {MIO} = \dfrac{{IO}}{{MI}} = \dfrac{{\dfrac{{a\sqrt 3 }}{4}}}{{\dfrac{a}{2}}} = \dfrac{{\sqrt 3 }}{2} \Rightarrow \widehat {MIO} = 30^\circ  \Rightarrow \widehat {MIN} = 60^\circ \)

Mà: \(\left( {AB,CD} \right) = \left( {IM,IN} \right) = \widehat {MIN} = 60^\circ \)

Đáp án cần chọn là: c