Câu hỏi
Thông hiểu
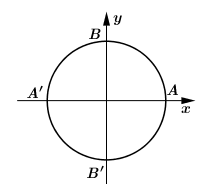
Cung lượng giác nào sau đây có mút trùng với \(B\) hoặc \(B'\)
Đáp án đúng: d
Phương pháp giải
Sử dụng lý thuyết: Cung lượng giác có số đo \(\alpha + \dfrac{{k2\pi }}{n}\) (hoặc \(a + \dfrac{{k{{360}^0}}}{n}\)) thì có \(n\) điểm biểu diễn.
Lời giải của Tự Học 365
Cung lượng giác có đầu mút trùng với \(B\) hoặc \(B'\) nghĩa là có hai điểm biểu diễn, do đó số đo có dạng \(\alpha + \dfrac{{k2\pi }}{2} = \alpha + k\pi \) hoặc \(a + {180^0}\). Loại A, B, C.
Ngoài ra số đo cung \(AB'\) bằng \( - {90^0}\) nên ta được \(a = - {90^0} + k{180^0}\).
Đáp án cần chọn là: d
Toán Lớp 12
