Câu hỏi
Vận dụng
Trên đường tròn với điểm gốc là \(A\). Điểm \(M\) thuộc đường tròn sao cho cung lượng giác $AM$ có số đo \({60^0}\). Gọi \(N\) là điểm đối xứng với điểm \(M\) qua trục \(Oy\), số đo cung lượng giác \(AN\) là:
Đáp án đúng: d
Phương pháp giải
- Xác định vị trí các điểm \(M,N\) và xác định góc hình học \(\widehat {AON}\) suy ra số đo cung lượng giác \(AN\)
Lời giải của Tự Học 365
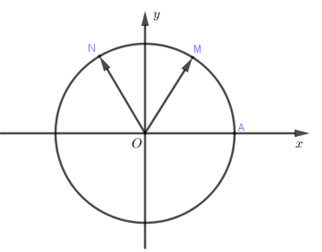
Ta có \(\widehat {AOM} = {60^0}\), \(\widehat {MON} = {60^0}\)
Nên \(\widehat {AON} = {120^0}\).
Khi đó số đo cung lượng giác \(AN\) bằng \({120^0} + k{360^0}\).
Đáp án cần chọn là: d
Toán Lớp 12
