Lời giải của Tự Học 365

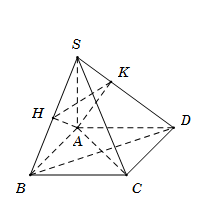
Từ $A$  kẻ $AH$ vuông góc với $SB\,\,\,\,\left( {H \in SB} \right).$

Ta có $\left\{ \begin{array}{l}SA \bot BC\\AB \bot BC\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AH$ mà $AH \bot SB$ suy ra $AH \bot \left( {SBC} \right) \Rightarrow AH \bot SC$

Từ A kẻ AK vuông góc với $SD\,\,\,\left( {K \in SD} \right),$ tương tự, chứng minh được $AK \bot \left( {SCD} \right) \Rightarrow AK \bot SC$

Khi đó $SC \bot \left( {AHK} \right)$ suy ra

$\widehat {\left( {\left( {SBC} \right);\left( {SCD} \right)} \right)} = \widehat {\left( {AH;AK} \right)} = \widehat {HAK} = {60^0}.$

Lại có $\Delta \,SAB = \Delta \,SAD\,\,\left( {c.g.c} \right) \Rightarrow AH = AK$ mà $\widehat {HAK} = {60^0}$ suy ra tam giác AHK đều.

Tam giác SAB vuông tại A có $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{B^2}}} = \dfrac{1}{{{x^2}}} + \dfrac{1}{{{a^2}}} \Rightarrow AH = \dfrac{{xa}}{{\sqrt {{x^2} + {a^2}} }} = AK = HK$

Suy ra $SH = \sqrt {S{A^2} - A{H^2}}  = \sqrt {{x^2} - \dfrac{{{x^2}{a^2}}}{{{x^2} + {a^2}}}}  = \dfrac{{{x^2}}}{{\sqrt {{x^2} + {a^2}} }} \Rightarrow \dfrac{{SH}}{{SB}} = \dfrac{{{x^2}}}{{{x^2} + {a^2}}}.$

Tương tự ta chứng minh được \(\dfrac{{SK}}{{SC}} = \dfrac{{{x^2}}}{{{x^2} + {a^2}}}\)

$ \Rightarrow HK$//$BD$ suy ra $\dfrac{{SH}}{{SB}} = \dfrac{{HK}}{{BD}} \Leftrightarrow \dfrac{{{x^2}}}{{{x^2} + {a^2}}} = \dfrac{{xa}}{{\sqrt {{x^2} + {a^2}} .a\sqrt 2 }} \Leftrightarrow \dfrac{x}{{\sqrt {{x^2} + {a^2}} }} = \dfrac{1}{{\sqrt 2 }} \Leftrightarrow 2{x^2} = {x^2} + {a^2} \Rightarrow x = a.$

Đáp án cần chọn là: c