Trong mặt phẳng $\left( P \right)$ cho tam giác đều $ABC$ cạnh $a$. Trên các đường thẳng vuông góc với mặt phẳng $\left( P \right)$ tại $B$ và $C$ lấy điểm $D,\,\,E$ cùng phía so với $\left( P \right)$ sao cho $BD = \dfrac{{a\sqrt 3 }}{2}$ và $CE = a\sqrt 3 $. Tính góc giữa hai mặt phẳng $\left( {ADE} \right)$ và $\left( {ABC} \right)$.
Phương pháp giải
Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng các hệ thức lượng trong tam giác vuông
Lời giải của Tự Học 365
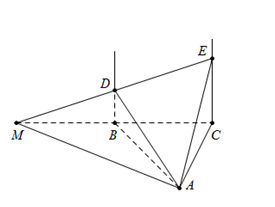
Vẽ $BC \cap DE = M$$ \Rightarrow \left( {ADE} \right) \cap \left( {ABC} \right) = AM$.
Ta có $BD$//$CE \Rightarrow \dfrac{{BD}}{{CE}} = \dfrac{{MB}}{{MC}} = \dfrac{1}{2} \Rightarrow BM = BC = BA$.
Suy ra $\Delta AMC$ vuông tại $A$ $ \Rightarrow AM \bot AC$.
$ \Rightarrow \left\{ \begin{array}{l}AM \bot AC\\AM \bot EC\end{array} \right. \Rightarrow AM \bot \left( {ACE} \right) \Rightarrow AM \bot AE \Rightarrow \Delta AME$ vuông tại $A$.
Và $\left\{ \begin{array}{l}\left( {ADE} \right) \cap \left( {ABC} \right) = AM\\\left( {ADE} \right) \supset AE \bot AM\\\left( {ABC} \right) \supset AC \bot AM\end{array} \right. \Rightarrow \widehat {\left( {\left( {ADE} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {AE;AC} \right)} = \widehat {EAC}$.
Xét $\Delta AEC$ vuông tại C, có $\tan \widehat {EAC} = \dfrac{{EC}}{{AC}} = \dfrac{{a\sqrt 3 }}{a} = \sqrt 3 \Rightarrow \widehat {EAC} = {60^0}$.
Đáp án cần chọn là: c
Toán Lớp 12
