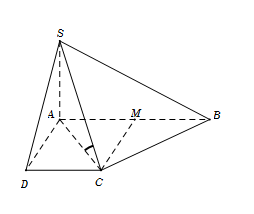
Cho hình chóp $S.ABCD$ có đáy là hình thang vuông $ABCD$ vuông tại $A$ và $D$, $AB = 2a,$ $AD = CD = a$. Cạnh bên $SA = a$ và vuông góc với mặt phẳng $\left( {ABCD} \right).$ Gọi $\varphi $ là góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABCD} \right)$ . Mệnh đề nào sau đây đúng?
Phương pháp giải
Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng các hệ thức lượng trong tam giác vuông
Lời giải của Tự Học 365
Gọi $M$ là trung điểm $AB$ $\, \Rightarrow ADCM$ là hình vuông.
Vì$\,CM = AD = a = \dfrac{{AB}}{2}$. Suy ra tam giác $ACB$ có trung tuyến bằng nửa cạnh đáy nên vuông tại $C$.
Ta có $\left\{ \begin{array}{l}BC \bot SA\\BC \bot AC\end{array} \right. \Rightarrow BC \bot \left( {SAC} \right) \Rightarrow BC \bot SC.$
Do đó :
$\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\\left( {SBC} \right) \supset SC \bot BC\\\left( {ABCD} \right) \supset AC \bot BC\end{array} \right. \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {SC;AC} \right)} = \widehat {SCA}.$
Tam giác $SAC$ vuông tại $A$$ \Rightarrow \tan \varphi = \dfrac{{SA}}{{AC}} = \dfrac{{SA}}{{\sqrt {A{D^2} + C{D^2}} }} = \dfrac{a}{{a\sqrt 2 }} = \dfrac{{\sqrt 2 }}{2}.$
Đáp án cần chọn là: a
Toán Lớp 12
