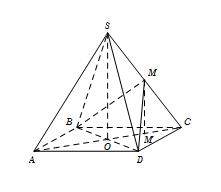
Cho hình chóp đều $S.ABCD$ có tất cả các cạnh bằng $a$. Gọi $M$ là trung điểm $SC$. Tính góc $\varphi $ giữa hai mặt phẳng $\left( {MBD} \right)$ và $\left( {ABCD} \right)$.
Phương pháp giải
Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng các hệ thức lượng trong tam giác vuông
Lời giải của Tự Học 365
Gọi M’ là trung điểm $OC \Rightarrow MM'\parallel SO \Rightarrow MM' \bot \left( {ABCD} \right).$
Theo công thức diện tích hình chiếu, ta có ${S_{\Delta \,M'BD}} = \cos \varphi .{S_{\Delta \,MBD}}$
$\begin{array}{l} \Rightarrow \cos \varphi = \dfrac{{{S_{\Delta \,M'BD}}}}{{{S_{\Delta \,MBD}}}} = \dfrac{{BD.M'O}}{{BD.MO}} = \dfrac{{M'O}}{{MO}} = \dfrac{{\dfrac{1}{2}OC}}{{\dfrac{1}{2}SA}}\\ = \dfrac{{\sqrt {B{C^2} - O{B^2}} }}{{SA}} = \dfrac{{\sqrt {{a^2} - {{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2}} }}{a} = \dfrac{{\sqrt 2 }}{2} \Rightarrow \varphi = {45^0}.\end{array}$
Đáp án cần chọn là: c
Toán Lớp 12
