Câu hỏi
Nhận biết
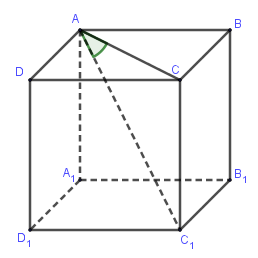
Cho hình lập phương \(ABCD.{A_1}{B_1}{C_1}{D_1}\). Gọi $\alpha $ là góc giữa $A{C_1}$ và mp$\left( {ABCD} \right)$. Chọn khẳng định đúng trong các khẳng định sau?
Đáp án đúng: b
Phương pháp giải
- Xác định hình chiếu của \(A{C_1}\) trên mặt phẳng \(\left( {ABCD} \right)\): chính là \(AC\).
- Góc giữa \(A{C_1}\) và \(\left( {ABCD} \right)\) là góc giữa \(A{C_1}\) và \(AC\).
Lời giải của Tự Học 365
Ta có
Ta có \({C_1}C \bot \left( {ABCD} \right)\) nên \(AC\) là hình chiếu của \(A{C_1}\) lên \(\left( {ABCD} \right)\)
\(\Rightarrow \widehat {\left( {A{C_1},\left( {ABCD} \right)} \right)} = \widehat {CA{C_1}} = \alpha \)\( \Rightarrow \tan \alpha = \dfrac{{C{C_1}}}{{AC}} = \dfrac{a}{{a\sqrt 2 }} = \dfrac{1}{{\sqrt 2 }}\).
Đáp án cần chọn là: b
Toán Lớp 12
