Cho hình lập phương\(ABCD.A'B'C'D'\). Gọi $\alpha $ là góc giữa $AC'$ và mp $\left( {A'BCD'} \right).$ Chọn khẳng định đúng trong các khẳng định sau?
Phương pháp giải
- Tìm giao điểm \(I\) của \(AC'\) với \(\left( {A'BCD'} \right)\).
- Tìm hình chiếu \(H\) của \(C'\) trên \(\left( {A'BCD'} \right)\) bằng cách tìm một đường thẳng qua \(C'\) mà vuông góc với \(\left( {A'BCD'} \right)\).
- Góc cần tìm là góc giữa \(C'I\) và hình chiếu \(HI\) của nó trên mặt phẳng \(\left( {A'BCD'} \right)\).
Lời giải của Tự Học 365
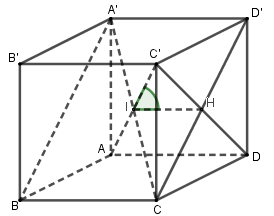
Gọi $\left\{ \begin{array}{l}A'C \cap AC' = I\\C'D \cap CD' = H\end{array} \right.$
mà \(\left\{ \begin{array}{l}C'D \bot CD'\\C'D \bot A'D'\end{array} \right. \Rightarrow C'D \bot \left( {A'BCD'} \right) \Rightarrow IH\) là hình chiếu vuông góc của \(AC'\) lên \(\left( {A'BCD'} \right) \Rightarrow \widehat {C'IH}\)là góc giữa \(AC'\) và \(\left( {A'BCD'} \right).\) Mà \(\tan \widehat {C'IH} = \dfrac{{C'H}}{{IH}} = \dfrac{1}{{\sqrt 2 }}.2 = \sqrt 2 .\)
Đáp án cần chọn là: d
Toán Lớp 12
