Cho tứ diện \(ABCD\) có \(AB,\,\,BC,\,\,CD\) đôi một vuông góc với nhau. Điểm nào dưới đây các đều bốn đỉnh \(A,\,\,B,\,\,C,\,\,D\) của tứ diện \(ABCD\) ?
Phương pháp giải
Nhận xét các tam giác \(ABD,BCD\) vuông rồi suy ra điểm cách đều bốn đỉnh của tứ diện.
Lời giải của Tự Học 365
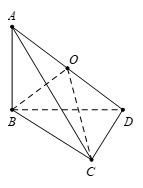
Ta có \(\left\{ \begin{array}{l}AB \bot BC\\AB \bot CD\end{array} \right.\,\, \Rightarrow \,\,AB \bot \left( {BCD} \right)\,\, \Rightarrow \) tam giác \(ABD\) vuông tại \(B.\)
Suy ra \(IA = IB = ID = \dfrac{{AD}}{2},\) với \(I\) là trung điểm của \(AD.\) \(\left( 1 \right)\)
Lại có \(\left\{ \begin{array}{l}AB \bot CD\\BC \bot CD\end{array} \right.\,\, \Rightarrow \,\,CD \bot \left( {ABC} \right)\,\, \Rightarrow \,\,\)tam giác \(ACD\) vuông tại \(C.\)
Suy ra \(EA = EC = ED = \dfrac{{AD}}{2},\) với \(E\) là trung điểm của \(AD.\) \(\left( 2 \right)\)
Từ \(\left( 1 \right),\left( 2 \right)\) suy ra \(I \equiv E\) nên trung điểm của cạnh \(AD\) cách đều \(A,\,\,B,\,\,C,\,\,D.\)
Đáp án cần chọn là: c
Toán Lớp 12
