Lời giải của Tự Học 365

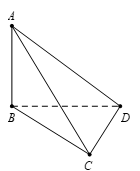
Ta có \(\left\{ \begin{array}{l}AB \bot BC\\AB \bot CD\end{array} \right.\,\, \Rightarrow \,\,AB \bot \left( {BCD} \right)\,\, \Rightarrow \) tam giác \(ABD\) vuông tại \(B.\)

Lại có \(BC \bot CD\) nên tam giác \(BCD\) vuông tại \(C.\)

Khi đó \(\left\{ \begin{array}{l}A{D^2} = A{B^2} + B{D^2}\\B{D^2} = B{C^2} + C{D^2}\end{array} \right. \Rightarrow A{D^2} = A{B^2} + B{C^2} + C{D^2} \Rightarrow AD = \sqrt {{a^2} + {b^2} + {c^2}} .\)

Đáp án cần chọn là: a