Lời giải của Tự Học 365

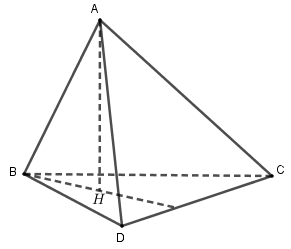
Vì \(AH\) vuông góc với \(mp\,\,\left( {BCD} \right)\) suy ra \(AH \bot CD.\)   \(\left( 1 \right)\)

Mà \(H\) là trực tâm của tam giác \(BCD\)\( \Rightarrow \,\,BH \bot CD.\)   \(\left( 2 \right)\)

Từ \(\left( 1 \right),\left( 2 \right)\) suy ra \(\left\{ \begin{array}{l}CD \bot AH\\CD \bot BH\end{array} \right. \Rightarrow CD \bot \left( {ABH} \right) \Rightarrow CD \bot AB.\)

Đáp án cần chọn là: d