Câu hỏi
Vận dụng
Cho hình chóp $S.ABCD$ có đáy $ABCD $ là hình bình hành. \(Mp\left( \alpha \right)\) qua $BD$ và song song với $SA$ cắt $SC$ tại $K.$ Chọn khẳng định đúng?
Đáp án đúng: c
Phương pháp giải
- Tính chất đường thẳng song song với mặt phẳng.
- Định lí đường trung bình của tam giác.
Lời giải của Tự Học 365
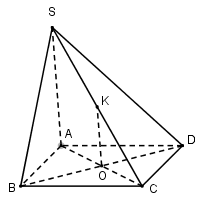
Gọi $O$ là giao điểm của $AC$ và $BD$
Trong mặt phẳng $SAC,$ qua $O$ kẻ ${\rm{O}}K \bot AC\,\,\left( {K \in SC} \right)$, suy ra $mp$\(\left( \alpha \right)\) chính là $mp(BDK).$
$OK // SA ; AO = OC$\( \Rightarrow \) $SK = KC.$ (Định lí đường trung bình của tam giác)
Đáp án cần chọn là: c
Toán Lớp 12
